The Exponential Secrets of Delay Scheduling: How a Few Seconds of Patience Make Big Data Flirt with Locality

Because sometimes it pays to wait before you make your move, Mesos-style: skip a few offers, get lucky with exponential odds.

Most people think of cluster schedulers as cold, efficient machines that push tasks around without emotion. But deep inside Mesos and Spark lives a scheduler with a surprisingly romantic side. It knows that great things happen when you wait just a little. Delay scheduling, in essence, is a story of patience and probability - it’s the tale of how a few seconds of restraint can make your data come running to you instead of the other way around.

Imagine a busy data center as a singles bar for tasks and nodes. Every node has something to offer - some are loaded with the data you crave, others are just pretending. A naive scheduler is the desperate one at the bar, throwing tasks at the first bartender node that smiles. Delay scheduling, on the other hand, is that calm, confident scheduler sipping its drink, saying, “Let’s wait a few seconds, maybe the perfect node will show up.” Statistically, it’s right.

When that ideal node finally appears, the scheduler sends over its function, maybe a sleek map, maybe a charming flatMap and the sparks fly, no pun intended. The computation happens locally, data transfer costs vanish, and network congestion melts away like awkward tension after a good joke. What looks like magic is really just exponential probability dressed in mathematical lingerie. The formula for locality, l(D), curves just like an attraction graph: steep at first, then leveling off as satisfaction nears 100%. Keep reading!

The beauty is that all this romance happens in milliseconds. The scheduler flirts, waits, and commits before anyone gets impatient. The compound interest limit quietly ensures that each skipped opportunity increases the chance of a perfect match, turning scheduling from a blind date into a calculated affair. So next time someone complains about waiting for resources, tell them it’s not latency, it’s the dopamine of expectation!

Behind the laughter lies a serious insight. In a world obsessed with instant execution, delay scheduling shows that strategic patience is not inefficiency, it’s intelligence. Just like in life, sometimes you have to say no to the first offer to end up in the right place - with your data and your cache still warm.

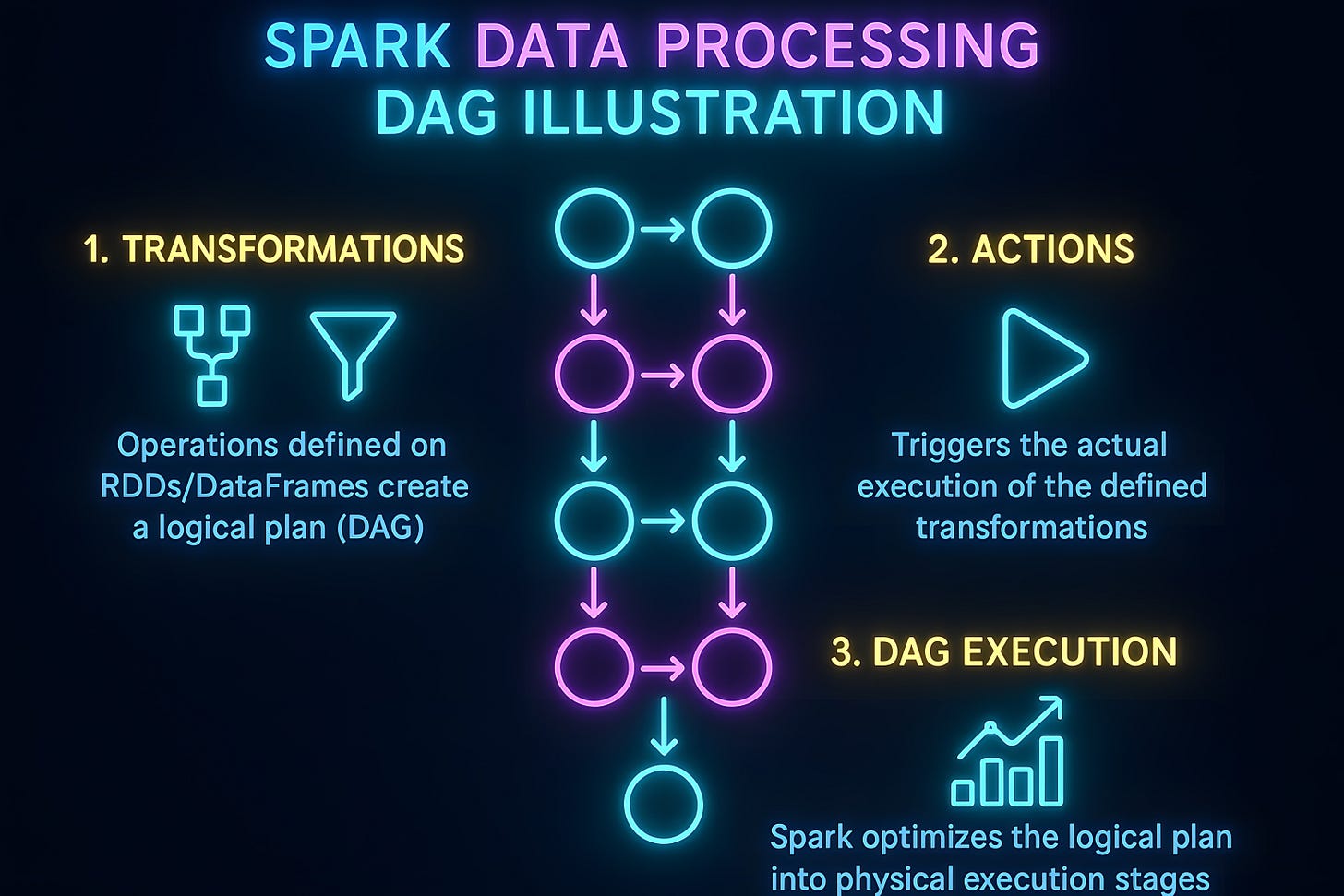
Tutorial modeling and bounding probabilities in cluster schedulers

We show how to turn an informal scheduling story into a clean probabilistic model that yields usable bounds. It mirrors the delay scheduling and Mesos setting, yet the pattern transfers to many systems.

1. Choose the time scale and decision granularity.
   Decide whether you model in task completions, in offer rounds, or in wall clock seconds. For delay scheduling, a natural choice is “opportunities,” one unit per offer you can accept or skip. Map back to seconds at the end using wait_time ≤ D × T / (L × M).

2. Define the state and the random experiment.
   Specify the variables you will treat as random. Common choices are node occupancy, task lengths, and the location of replicas. For a single job, represent the set of preferred nodes at stage k by a random subset of the M nodes.

3. Encode the event of interest.
   Write the event in plain set form. Example, “no local slot appears in the next D opportunities” becomes the intersection of D independent failures. The probability then factors cleanly if you justify independence or negative correlation.

4. Start with exact expressions, then simplify.
   For locality with patience D, the exact per-opportunity success probability is p. The chance of seeing at least one success in D tries is 1 − (1 − p)^D. When p itself varies with k, keep the k index for now and plan to average later.

5. Translate structure into p.
   Express p in terms of system parameters. With R-way replication and k remaining blocks, a node is useful unless all R replicas of all k blocks lie elsewhere. That yields p(k) = 1 − (1 − k/M)^R under random placement. If your system breaks this assumption, adjust p by measurement or by a coupling argument that upper or lower bounds it.

6. Move from stage to lifetime.
   Jobs evolve, so average stagewise locality over k from 1 to N. This gives l_exact(D) = 1 − (1/N) × sum_{k=1..N} (1 − k/M)^(R D). You now have a precise quantity that is easy to evaluate numerically and already useful for planning.

7. Replace hard-to-handle powers by exponentials.
   Use the elementary inequality (1 − x) ≤ exp(−x) for x in [0, 1]. Apply it with x = k/M to get a bound that is smooth in the parameters. Consider the following example.
   L_k(D) = 1 − (1 − k/M)^(R D) ≥ 1 − exp(−R D k / M).
   Averaging over k yields a closed-form lower bound on l(D) via a geometric series.

8. Invert the bound to size the policy.
   Many controls are chosen by targets. If you want l(D) ≥ λ, solve the inequality for D. Using the standard geometric series approximation gives D ≥ −(M/R) × ln( ((1 − λ) × N) / (1 + (1 − λ) × N) ). This is conservative, so the realized locality will be at least λ, often higher.

9. Map opportunity counts to time budgets.
   Schedulers run in real time. Convert D to seconds with wait_time ≤ D × T / (L × M). This keeps the policy grounded and ensures you do not trade locality for utilization beyond a few seconds.

10. Add safety checks with simple concentration tools.
    When you worry about variance or hotspots, apply basic bounds. The union bound turns “any of J bad things happen” into a sum of J small probabilities. Chernoff or Hoeffding bounds control fluctuations of sums of independent indicators when you aggregate over many opportunities or many nodes. If independence is imperfect, lean on negative correlation folklore for placement without replacement, or use empirical p(k) from logs and plug it into the same algebra.

Define opportunities as offer rounds, encode the success event “local in ≤ D rounds,” express p(k) from replication and remaining blocks, average over k to get l_exact(D), relax to exponentials for a closed form, invert to pick D for a target λ, and translate D to seconds. Validate p(k) with a short trace study if your cluster is skewed. If you detect long-task hotspots, keep the patience windows short, rely on averaging across stages, and consider a second tier for rack-local with a smaller patience since the number of racks is much smaller than the number of nodes.

If tasks have a spread of durations, treat opportunity arrivals as a renewal process with mean interarrival T / S, then apply the same counting argument using Wald’s identity in words. If multiple jobs contend for the same hot files, update p(k) to reflect conditional availability or introduce a throttle that reduces the chance that all R replicas sit behind long tasks. The bounding pattern does not change, only the expression for p(k) changes.

This tutorial leaves you with a repeatable path. State the event precisely, pick a reasonable independence or correlation model, derive an exact probability, relax to an exponential for algebraic clarity, invert to size the control, then map the control to seconds so the operator can deploy it with confidence.

Deriving the job-locality curve l(D), and why a few seconds of patience go a long way

We show how to consolidate the delay scheduling model and the Mesos execution architecture into one clean derivation. The goal is to express job locality, written as l(D), as an explicit function of a small patience parameter D that allows a framework to skip a few non-local opportunities before it launches a task. You can then read off how many deferrals you need to hit a target locality and how that maps to real time waits in a cluster.

Model and notation

Consider a cluster with M nodes and L concurrent task slots per node, so the total number of slots is S = M × L. Average task duration is T. A job has N tasks that read blocks replicated R times across the cluster. While k tasks remain to be scheduled, we write p(k) for the fraction of nodes that hold at least one of those k blocks. Under random independent placement, a node misses all k blocks only if all R replicas of every block are elsewhere. The fraction of nodes that are useful to the job is then the following as derived from the basic probability formula.

p(k) = 1 − (1 − k/M)^R.

Delay scheduling adds a small patience window. When a scheduling opportunity arises on a node that does not hold the next block, the job can defer, up to D times, before giving up and running non-local. If the chance a single opportunity is local is p, the chance that at least one of the next D opportunities is local is 1 − (1 − p)^D.